Modelo pioneiro de calculadora da Facit, que substituiu as manivelas por motores elétricos

As calculadoras eletrônicas começaram a aparecer no final da década de 60. E, pelos recursos oferecidos e facilidade de operação, logo tomaram conta do mercado. Até essa época, existiam máquinas de somar, seja de alavanca ou elétricas, que executavam somas, subtrações (adição de números negativos) e multiplicação (através de adições sucessivas).

Mas a divisão era um problema, devido ao tratamento do resto. Uma solução inteligente para a divisão foi desenvolvida pela empresa sueca Facit, que usava adições e subtrações sucessivas, acionadas por manivelas.

Para a soma e multiplicação, girava-se a manivela no sentido horário (no caso da multiplicação, uma volta para cada unidade do multiplicador, o que era marcado em um visor separado). Para a divisão, a manivela era girada diversas vezes no sentido anti-horário.

Quando o resto – que aparecia em um dos visores – ficava negativo, era acionada uma campainha. Então, bastava só retornar a manivela uma volta, que o quociente aparecia em um dos visores.

A máquina era de acionamento puramente manual, o que surpreende os mais jovens. Como as demais, utilizava componentes mecânicos, que a tornavam pesada e grande.

Posteriormente, a Facit lançou uma versão que substituía as manivelas por motores elétricos (uma brincadeira interessante era fazer uma divisão por zero, o que fazia com que a máquina ficasse rodando indefinidamente, até ser desligada). Havia ainda algumas calculadoras de contabilidade, porém, ainda maiores e mais pesadas.

RÉGUAS

Isso tudo tornava bem mais comum a utilização da régua de cálculo para operações mais complexas. Tratava-se de uma ferramenta mais leve de trabalho, com uma grande quantidade de recursos. As réguas iam desde pequenos modelos de bolso, com poucas funções, até modelos maiores, com cerca de 30 cm e muitos recursos. Os modelos de bolso tinham uma quantidade menor de recursos.

Para a utilização da régua de cálculo, o importante é que as escalas sejam lidas com rapidez e segurança. O intervalo de leitura diminui à medida que se avança na escala, ou seja, o espaço entre 1 e 2 é maior que o espaço entre 5 e 6.

O valor 2 de uma escala pode significar, por exemplo, 2 m, 20 cm, 0,02 m etc. Ou seja, não há indicação sobre onde se deve colocar a vírgula. A linha do cursor é muito fina, o que dá razoável precisão de leitura, mesmo quando cai entre dois valores.

Por essa razão, é importante ter a ordem de grandeza (0,2, 2, 20, 200 ou 2 mil) do resultado que se está calculando.

Ilustração mostra o anverso e reverso de um modelo bastante difundido nos anos 60

Essa ideia, embora simples, deixou de ser usada depois que as calculadoras passaram a fazer o serviço. No entanto, os erros continuaram a se repetir, pois é comum as pessoas fazerem o cálculo e chegarem a resultados errados.

FUNCIONAMENTO

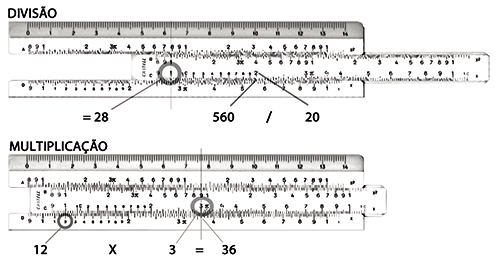
O funcionamento da régua se baseia na soma de segmentos. Para tanto, a ferramenta é formada por duas réguas fixas e uma corrediça. Para se fazer uma multiplicação (12 x 8, por exemplo), somam-se dois segmentos das escalas logarítmicas.

Na régua, coloca-se o valor 1 da escala C (móvel) sobre o valor 1,2 (ou 12) da escala D. Correndo o cursor até o valor 8 da escala C, pode-se ler o resultado na mesma vertical da escala D (9,6). Se pensarmos em 10 x 8, saberemos que a ordem de grandeza é 80 e, portanto, o resultado será 96.

Para a divisão, o processo é similar, subtraindo os segmentos (560/20, por exemplo): nesse caso, alinhamos o valor 5,6 da escala D com o valor 2 da escala C. O resultado estará na escala D, debaixo do valor 1 da escala C (2,8). Como a ordem de grandeza é 500/20=25, o resultado da operação será 28.

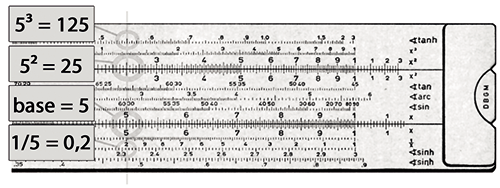
Existem também algumas escalas de leitura direta, todas referidas à escala D, por exemplo, quadrados (A), cubos (K), inverso (DI). Assim, se colocarmos o cursor em 2 na escala D, podemos ler diretamente 4 na escala A, 8 na escala K e 5 (0,5) na escala DI. Evidentemente, se entrarmos com o valor na escala de cubos (K), poderemos ler a raiz cúbica na escala D.

O cursor de algumas réguas possui uma marca auxiliar que permite a conversão de kw em hp. Além desses recursos, existem escalas de funções trigonométricas (sen, tg, senh, tgh, arc) e um conjunto de escalas “e”, que permite elevar qualquer número a outro número (por exemplo, 3,4^5,6).

Funcionamento da régua de cálculo baseia-se na soma de segmentos

Para isso, basta colocar o valor 1 da escala C no valor da base, deslocar o cursor até o expoente e fazer a leitura na escala correspondente. O cosseno e a cotangente de um ângulo α são o seno e a tangente do ângulo complementar (90-α).

Para facilitar a operação (pois às vezes o valor da régua móvel ficava fora da escala e obrigava a repetir a operação no outro sentido), havia outro par de escalas similar à C e D, deslocado de π (escalas CF e DF). Em algumas réguas, existe uma marca “C” na escala C.

Se colocarmos o diâmetro de um círculo na escala D e fizermos coincidir com a marca C da escala C, teremos a área do círculo na escala A, acima da marca 1 da escala B.

Existiam também algumas réguas especializadas para, por exemplo, cálculos eletrotécnicos (rendimento de motores, queda de tensão etc.). Tudo isso parece muito complicado, mas era uma simples questão de prática.

Por muito tempo, a régua era distribuída como brinde, como faz ainda hoje com calculadoras

RÉGUA BÁSICA

Essa régua era distribuída como brinde, como se faz hoje com calculadoras. Possuía no anverso as escalas C e D, para multiplicação e divisão, as escalas defasadas de π, uma escala em mm e, no reverso, dois nichos para cálculo das funções trigonométricas, com escalas S, L e T na régua móvel.

Para determinar-se os valores dos senos e tangentes, bastava colocar o ângulo em graus na escala S (coincidindo com a marca do nicho menor ou maior) e ler o valor do seno na escala B, abaixo do valor 1 da escala A.

O cosseno e a cotangente são o seno e a tangente do ângulo complementar (90-α). A solução possuía ainda a marca C e uma escala de quadrados de leitura direta.